In this work we show how the estimation of quantities can be made much more efficient by using information on the moments of the process.
This is done via the technique of control variates, which is essentially a random variable that is correlated with the variable of interest. The control variate technique allows to leverage this correlation by adjusting the final estimate according to the sampled value of the control variate.
In a chemical reaction network the moment \(E(X_t^m)\) over time is given by
\[\frac{d}{dt}E(X_t^m)=\sum_j \left( \left( {(X_t - v_j)}^m - X_t^m \right) \alpha_j(X_t) \right)\]From this one can, by integration derive
\[0 = E({f(X_{T})}) - e^{\lambda T}E({f(X_{t_0})}) + \sum_{k}c_k\int_{t_0}^{T}e^{\lambda(T-t)}E({X_t^{m_k}})\,dt\,.\]The random variable implied by the expectation above is correlated with the expected value of the process at time \(T\). Using it as a control variate we often can reduce the variance of the final estimator considerably:
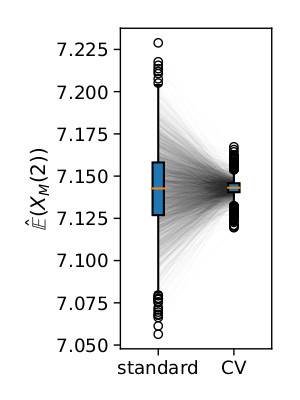
The pre-print is available on arXiv.